のむのむのconsole.log

Arduino + 昇圧チョッパー回路で5Vから12Vを作る

Arduino 電子工作電子回路

さて、お久しぶりです。今日は珍しく電子工作です。今回作成した回路は昇圧チョッパー回路です。

f:id:nomunomu0504:20190421000134j:plain:w500

昇圧チョッパー回路

降圧チョッパー回路は聞いたことがあるかもしれませんが、『降圧』ではなく『昇圧』です。

一般的な昇圧チョッパー回路では、以下のようにMOSFETを用いると思うんですが

f:id:nomunomu0504:20190420235007p:plain

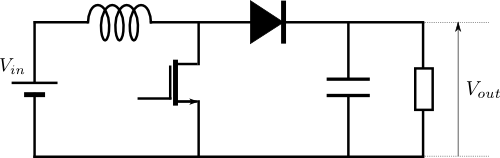
手元になかったので一般的なトランジスタを用いて回路を作成しました。

f:id:nomunomu0504:20190421012921p:plain

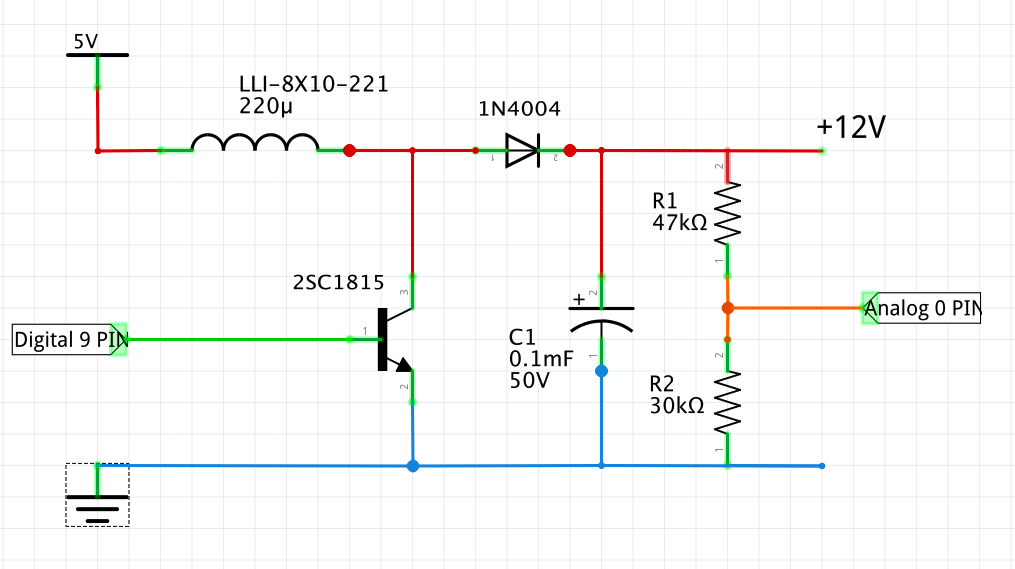
この回路に入力するのはもちろんArduinoからの5V

f:id:nomunomu0504:20190421000100j:plain:w500

そして、昇圧後の電圧を測定すると....

f:id:nomunomu0504:20190421000027j:plain:w500

無事昇圧できているのを確認できました！！🎉

この後は、この回路の計算をしてみたいと思います。

昇圧チョッパー回路の計算

計算するために、先ほどの昇圧チョッパー回路に以下のようなパラメータを振ります。

f:id:nomunomu0504:20190421013859p:plain

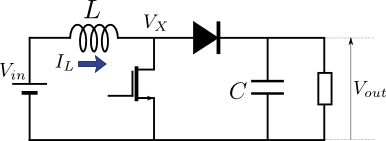
このとき 『定常状態においてインダクタ両端の周期平均電圧が等しくなる』 という性質を用いる。

すると、上記の図の ${ V_{in} }$ の時間平均（ここでは ${ V_{in} }$ は時間によって変化しないので ${ V_{in} }$ そのもの）が ${ V_{in} }$ の周期時間平均と同じになるので、

$\displaystyle V_{in} = \frac{1}{T_s} \int_{\tau}^{\tau + T_s} V_X dt$

とすることができる。以下のように波形がなっているとすれば、

f:id:nomunomu0504:20190421020301p:plain

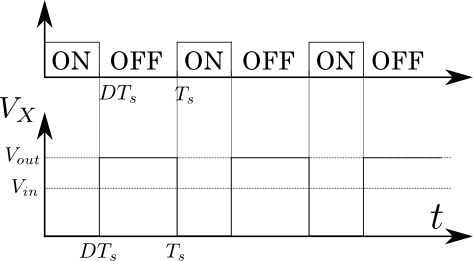
上記の波形から、全体における0Vの割合はDである。また ${ V_{out} }$ になっている時間は（1-D）と表すことができるので、その平均電圧 $\overline{V}_{X}$ は

$\overline{V}_{X}= \left({1-D}\right)V_{out}$

と計算できる。これと、先ほどの式より

$V_{in} = \left({1-D}\right)V_{out}$

となるので、 $V_{out}$ について方程式を解けば、

$\displaystyle V_{out}= \frac{1}{1-D}V_{in}$

が得られる。ここで、今回の場合は $V_{out}$ 部分で抵抗をR2: 30kΩ、R1: 47kΩを用いているので、

$\displaystyle V_{out}= \frac{1}{\frac{R2}{R1 + R2}}V_{in}$

となる、それぞれに値を当てはめ計算すると、

$\displaystyle \begin{align} V_{out} &= \frac{1}{\frac{R2}{R1 + R2}}V_{in} \\ \\ &= \frac{R1 + R2}{R2}V_{in} \\ \\ &= 5\frac{(47 + 30) \cdot 10^3}{30 \cdot 10^3} \\ \\ &= 12.8\dot{4} \\ \end{align}$

となり、実際の実験結果12.79Vに近い値となっていることが分かります😇🎉

今日はここまで！